1591. Задача сапожника
Сапожнику
необходимо выполнить n работ. Каждый
день сапожник может выполнять только одну работу. Для каждой i - ой работы известно время ее
выполнения Ti и штраф Si, который каждый день должен
платить сапожник до тех пор, пока он не отдаст i - ую работу заказчику. Найти последовательность выполнения работ,
при которой сумма штрафа будет минимальной.
Вход. Состоит из нескольких тестов. Первая строка
каждого теста содержит количество работ n
(1 £ n
£ 1000), за которой следуют n строк, содержащие характеристики работ
Ti (1 £ Ti
£ 1000) и Si (1 £ Si £ 10000).
Выход. Для каждого теста в отдельной строке вывести
порядок работ, при котором сумма штрафа минимальна. При существовании
нескольких оптимальных порядков работ выводить лексикографически наименьший.
|
Пример входа |
Пример выхода |
|
4 3 4 1
1000 2 2 5 5 |
2 1 3
4 |
РЕШЕНИЕ
жадный
алгоритм
Анализ алгоритма
Рассмотрим две
работы с характеристиками T1, S1 и T2, S2.
Если сначала
будет выполняться первая работа, а потом вторая, то сумма штрафа составит
S1
* T1 + S2 * (T1 + T2)
Если за второй
будет выполняться первая работа, то в качестве штрафа следует заплатить
S2
* T2 + S1 * (T1 + T2)
Рассмотрим, при
каком условии сумма штрафа при выполнении работ 1, 2 лучше, нежели при
выполнении работ в порядке 2, 1:
S1
* T1 + S2 * (T1 + T2) < S2
* T2 + S1 * (T1 + T2)
Раскроем скобки
и приведем подобные:
S2
* T1 < S1 * T2
Или то же самое,
что
.
Пусть теперь
имеется n работ. Если существуют i - ая и j - ая работы, для которых Ti
/ Si > Tj / Sj, то поменяв их местами в последовательности
выполнения, мы уменьшим общую сумму штрафа. Таким образом, для минимизации
штрафа следует отсортировать работы по неубыванию отношения времени их
выполнения к сумме штрафа.
В случае
равенства отношения (Ti /
Si = Tj / Sj),
работы следует сортировать по возрастанию их номеров.
Пример
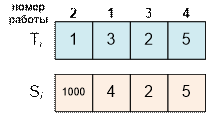
Отсортируем
работы по неубыванию отношения времени их выполнения к сумме штрафа:
Получим
соответственно оптимальный порядок выполнения работ, указанный в примере. Третья и
четвертая работы имеют одинаковые отношения (2 / 2 = 5 / 5), поэтому
располагаем их в порядке возрастания номеров работ.
Реализация
алгоритма
Информацию о
работах будем заносить в массив jobs, элементами которого являются вектора
длины 3. После считывания данных jobs[i][0]
содержит время выполнения i - ой
работы Ti, jobs[i][1] содержит значение штрафа Si, а jobs[i][2] содержит номер работы i.
vector<int> j(3,0);
vector<vector<int> > jobs;
Функция сортировки. Сравнение 
эквивалентно a[0] *
b[1] < b[0] * a[1]. Если отношения a[0] / b[0] и a[1] / b[1] равны, то
раньше должна следовать работа с меньшим номером. Поэтому в этом случае следует
сравнивать номера работ, которые содержатся в a[2] и b[2].
int
lt(vector<int> a, vector<int> b)
{
if (a[0] *
b[1] == b[0] * a[1]) return a[2] < b[2];
return a[0] *
b[1] < b[0] * a[1];
}
Основная часть программы. Читаем входные данные. Заполняем
массив jobs.
while(scanf("%d",&n) == 1)
{
jobs.clear();
for(i = 1; i
<= n; i++)
{
scanf("%d
%d",&j[0],&j[1]); j[2] = i;
jobs.push_back(j);
}
Сортируем работы согласно компаратору
lt.
sort(jobs.begin(),jobs.end(),lt);
Выводим результат как требуется в
условии задачи.
for(i = 0;
i < n; i++)
printf("%d ",jobs[i][2]);
printf("\n");
}
Реализация при
помощи класса
#include <cstdio>
#include <algorithm>
#define MAX 1010
using namespace std;
int
i, n, t, fine, tests;
class
Work
{
public:
int time,
fine, id;
Work (int
time = 0, int fine = 0, int id = 0) :
time(time), fine(fine), id(id) {};
};
Work
*Jobs;
int
f(Work a, Work b)
{
// a.time
b.time
// ------ < ------
// a.fine
b.fine
if (a.time *
b.fine == b.time * a.fine) return a.id <
b.id;
return a.time
* b.fine < b.time * a.fine;
}
int
main(void)
{
while(scanf("%d",&n) == 1)
{
Jobs = new
Work[n];
for(i = 0;
i < n; i++)
{
scanf("%d
%d",&t, &fine);
Jobs[i] = Work(t,fine,i+1);
}
sort(Jobs,Jobs+n,f);
for(i = 0;
i < n; i++)
printf("%d ",Jobs[i].id);
printf("\n");
delete[]
Jobs;
}
}
Java реализация
import java.util.*;
class Job
{
int s, t, id;
public Job(int s, int t, int id)
{
this.s = s;
this.t = t;
this.id = id;
}
}
public class Main
{
public static class MyFun implements Comparator<Job>
{
public int
compare(Job a, Job b)
{
if (a.s * b.t == b.s * a.t) return a.id - b.id;
return a.s * b.t - b.s * a.t;
}
}
public static void
main(String[] args)
{
Scanner con = new Scanner(System.in);
while(con.hasNext())
{
int n = con.nextInt();
ArrayList<Job> jobs = new ArrayList<Job>();
for(int i = 1; i <= n; i++)
{
int s = con.nextInt();
int t = con.nextInt();
jobs.add(new Job(s,t,i));
}
Collections.sort(jobs, new MyFun());
for(int i = 0; i < n; i++)
System.out.print(jobs.get(i).id + " ");
System.out.println();
}
con.close();
}
}